Problemas entre conjuntos, Relaciones binarias y sus propiedades. Ejemplos, videos y ejercicios.

 Problemas entre conjuntos: Son problemas que debemos solucionar por medio de conjuntos para determinar cantidades exactas.

Por ejemplo

En una aula hay 60 alumnos de los cuales a 7 no les gusta ni geometría ni aritmética y a 35 les gusta sólo aritmética ¿Cuántos les gusta geometría, si los que le gusta ambos cursos son 1O?

Los estudiantes que les gusta solo geometría son 8 estudiantes

En una encuesta realizada a 160 personas,

94 tienen refrigeradora, 112 tienen cocina a gas y 1O no tienen ninguno de los artefactos

mencionados. ¿Cuántos tienen cocina gas solamente?

Debemos restar el total de personas que tienen cocina a gas con la intersección. 56 personas tienen solo cocina a gas

Relaciones binarias y sus propiedades

¿Qué es relación?

Dados dos conjuntos A y B, se llama relación R de A en B a todo subconjunto del pro­ducto cartesiano A x  B, donde los pares ordenados (a, b) cumplen alguna condición.

Se denota: R: A ---7 B, y se lee: R es una relación de A en B, donde A es el conjunto de partida y B es el conjunto de llegada.

Una correspondencia de un conjunto A consigo mismo, que relaciona sus ele­mentos con un criterio dado recibe el nombre de relación binaria R.

¿Qué es una relación binaria?

La relación binaria es una relación matemática entre dos elementos de dos conjuntos o de un elemento consigo mismo

Propiedades de la relación binaria

Ejemplos de problemas entre conjuntos

Relaciones binarias

Videos para reforzar

Diagramas de Venn operaciones entre dos y tres conjuntos

Diagrama de Venn de dos conjuntos

Diagrama de Venn de tres conjuntos

Operaciones entre conjuntos

Intersección: Es lo que tienen en común esos conjuntos y su símbolo es "∩"

A=(m, n, o, p, q) B=(o, p , q r, s)

A ∩ B=(o, p, q)

Unión: Es la unión de dos o mas conjuntos y su símbolo es "U"

La unión de dos conjuntos A y B es el conjunto formado por los elementos que pertenecen a A o que pertenecen a B

A=(1, 2, 3) B=(a, b, c)

A U B= (1, 2, 3, a, b, c)

Diferencia: Son los elementos que le pertenecen solo a ese conjunto sin contar la intersección y su símbolo es " - "

A=(1, 3, 7) B= (7, 9, 13)

A- B=(1, 3)

Complemento: Es lo que le falta a un conjunto para ser el conjunto universo

A: (1, 2, 3) B=(3, 4, 5, 6)

A'=(4, 5, 6)

Evaluaciones de las formulas lógicas

 Tablas de Verdad

Las tablas de verdad nos muestran los posibles resultados de cualquier fórmula lógica. Una formula lógica puede tener de resultado una contingencia, una tautología o una contradicción

Contingencia: Resultados verdaderos y falsos

Tautología: Resultados verdaderos

Contradicción: Resultados falsos

¿Cómo llenar una tabla de verdad con mas de dos proposiciones?

🧶 Debemos primero saber cuantas proposiciones hay

🧶 Luego aplicamos la fórmula 2^{n}, n es el número de proposiciones que hay `

Por ejemplo

p, q, r             2 al cubo = 8

🧵 Entonces en p se ubicarían la mitad del resultado principal (2 al cubo= 8) entonces 4 Verdaderos y 4 Falsos

🧵 Después la mitad de la proposición anterior (4) entonces 2 Verdaderos y 2 Falsos

🧵 Después la mitad de la proposición anterior (2) entonces 1 Verdadero y 1 Falso

 Y se realizan las operaciones correspondientes ya sea conjunción, disyunción, implicación, equivalencia o negación

Conjuntos y sus operaciones

 ¿Qué es un conjunto?

Un conjunto es una agrupacion de elementos. 

¿Qué es un elemento?

Un elemento es cada objeto que forma parte de un conjunto

Clasificacion de los conjuntos según sus elementos

Finitos: tienen fin

Por ejemplo: el abecedario, las vocales, etc

Infinitos: no tienen fin

Por ejemplo: los numeros, las estrellas, etc

Unitario: tienen un solo elemento

Por ejemplo: una manzana, un balón, etc

Vacio: no tiene elementos

Universo: tiene todos los elementos

A= (a, b, c) B=(d, c, f)

Conjunto universo: (a, b, c, d, f)

Conjuntos por compresión

Es la caracteristica que los define 

A= (2,4,6,8)

Por compresion se escribiria 

(x/x es un numero par x<10)

B= (Lunes, martes, miercoles, jueves, viernes, sabado, domingo)

Por compresion se escribiria 

(x/x es un dia de la semana)

Conjuntos por extensión

Es representar esa caracteristica

(x/x es un numero par x<10)

Hay que escribir los numeros pares que sean menor que 10

A=(2, 4, 6, 8)

(x/x es un dia de la semana)

Hay que escribir los dias de la semana

B= (Lunes, martes, miercoles, jueves, viernes, sabado, domingo)

Simbolos que se usan en los conjuntos

∈= Pertenece

∈/=No pertenece

>= Mayor que

<= Menor que
≥= Mayor o igual que

≤= Menor o igual que

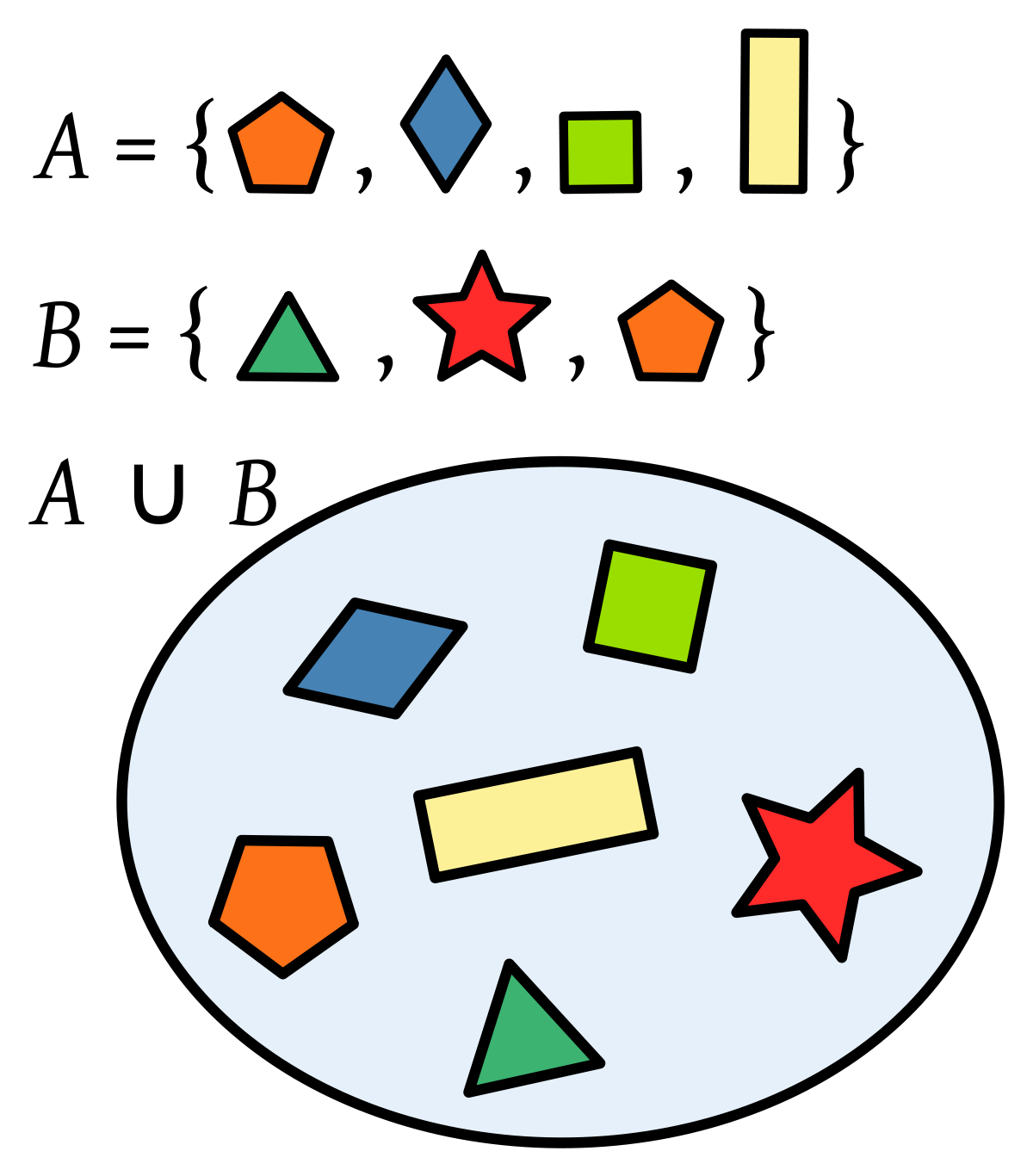
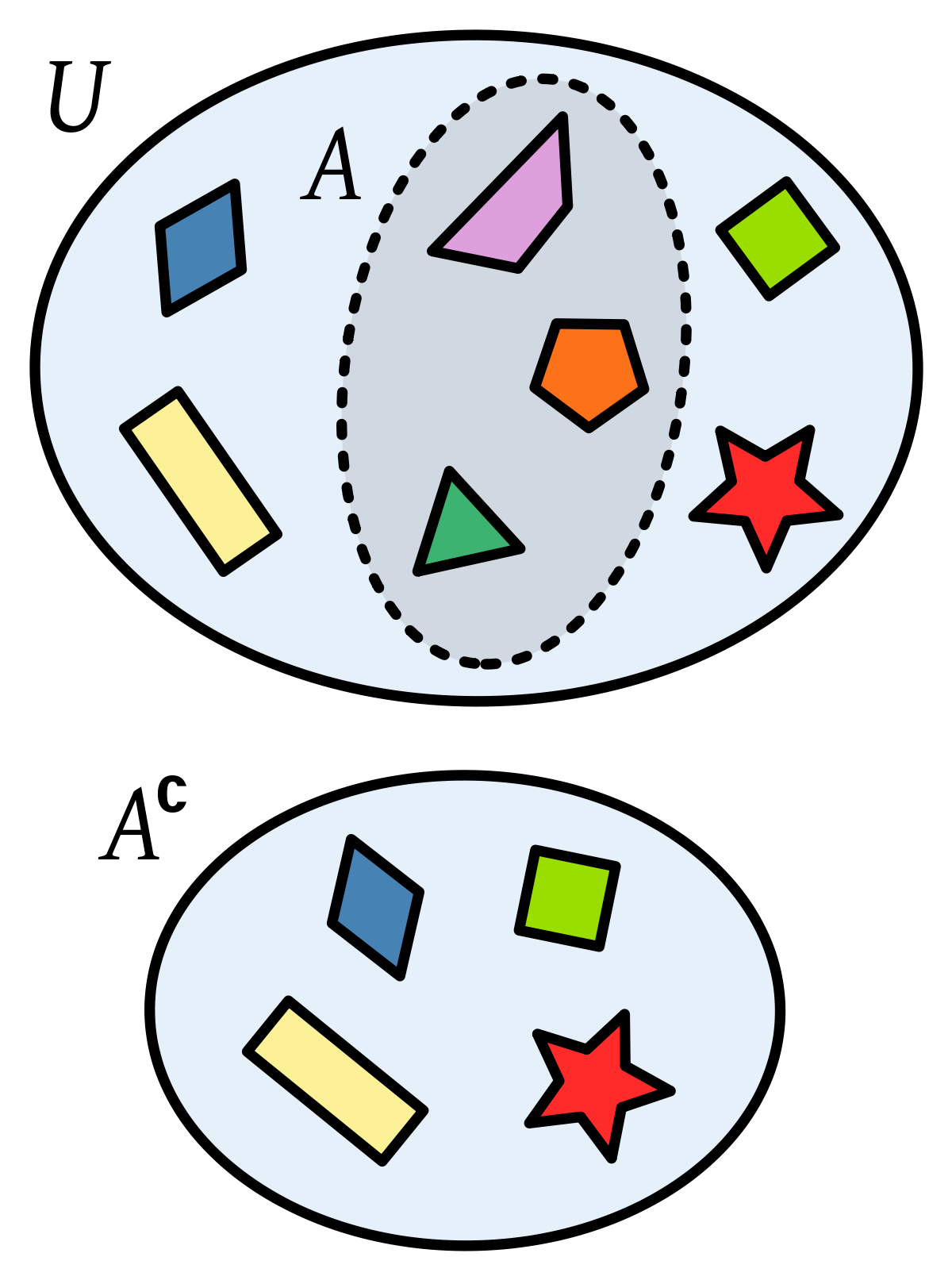
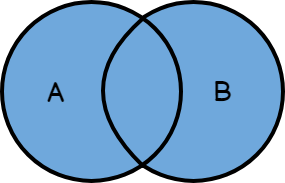
Representación grafica de las operaciones entre conjuntos

Unión

Intersección

Diferencia

Complemento

Proposiciones compuestas🎫

Son mas de dos proposiciones que pueden estar separadas por conectivos lógicos como: y, o, si...entonces, si y solo si

 Conjunción🎫

La conjunción se representa simbolicamente con ∧ y  como expresión es "Y"

En la tabla de verdad de la conjunción solo es verdad cuando ambas proposiciones son verdaderas, el resto es falso

Disyunción🎫

La disyuncion se representa simbolicamente ∨ y se como expresión es "O"

En la disyuncion solo debe haber una proposicion verdadera para que el resultado sea verdadero y solo F ∨ F es falso

Condicional o Implicación

La implicacion se representa simbolicamente ⇒ y se como expresión es "si...entonces"

En la implicacion solo es falso cuando empieza con verdad y termina con falso depeus todo es verdadero

Bicondicional o Equivalencia

La equivalencia se representa simbolicamente ↔  y se como expresión es "si y solo si"

En la equivalencia solo es falso cuando hay uno verdadero y una falso o una falso y uno verdadero pero si hay dos verdaderos o dos falsos la respuesta es verdadero

Negación

Cuando es verdadro y lo niegan se convierte en falso y cuando es falso y lo niegan se convierte en verdadero

Tabla de verdad 

Lógica proposicional (Proposiciones simples y compuestas)

¿Qué es lógica proposicional?🎁

Es un lenguaje claro que estudia las proposiciones y tiene como objetivo diferenciar a los correctos de los incorrectos.

¿Qué es una proposición?🎁

Es una expresión que puede ser verdadero o falso. Para enumerar las proposiciones se lo hace con letras minúsculas

¿Cuáles son proposiciones?🎁

Son las oraciones afirmativas o negativas. Por ejemplo

p) El cielo es azul

q) La luna no es una estrella

r) Los animales hablan

s) El futbol es un deporte

¿Cuáles no son proposiciones?🎁

Las preguntas, las exclamaciones no son consideradas proposiciones. Por ejemplo

p) ¿Cuál es tu nombre?

q) ¡ Ayuda!

r) ¿Qué estas haciendo?

s) ¡Ven!

¿Quién es el Padre de la lógica matemática?🎁

El padre de la lógica matemática es Aristóteles

¿Cuáles son monódicas y cuales son diádicas?🎁

A la negación se le conoce como monódica porque se aplica solo a una oración y se le conoce como diádicas cuando se le aplica una proposición compuesta a 2 oraciones o más.

¿Qué es una proposición compuesta?

Es la unión de varias proposiciones simples unidas por un conector lógico

¿Qué es un conector lógico?

Son palabras que se usan para conectar varias proposiciones. Por ejemplo Y, O, Si...entonces, Si y solo si...

Ejemplos de proposiciones compuestas

• En primavera hay flores y en invierno hay nieve
• Luis es responsable o irresponsable

Ejercicios

Racionalizacion con denominadores monomios y binomios

 ¿Qué es racionalizar?📑

La racionalización consiste en eliminar los radicales del denominador.📜

¿Como racionalizar con denominador monomio?📑

🔔 Primero hay q identificar si en el denominador hay una raiz y ver cual es, en este caso la raiz es 3.

🔔 Segundo hay que multiplicar al denominador y numerador por la raiz del denominador y asi hacer que el denominador se convierta en cuadrado.

🔔 Tercero hay que multiplicar: en el numerador se multplica 5*√3=5√3 y en el denominador se multiplica √3*√3=√3²  .

🔔 Cuarto hay que quitar la raiz en el denominador: la raiz se simplifica con el cuadrado y quedaria 3.

¿Como racionalizar con denominador binomio?📑

🔔 Primero hay que confirmar que hayan raices en el denominador y saber si es un monomio o un binomio, en este caso es un binomio asi que hay que aplicar los productos notables, es decir que hay que ubicar el contrario que seria √3 - √5.

🔔 Segundo hay que multiplicar al numerador y al denominador por √3 - √5.

🔔 Tercero, despues de multiplicar los terminos quedaria asi, ahora se debe sacar los terminos del denominador de la raiz.

🔔 Cuarto, ya que ya se simplifico la raiz y los cuadrados en el denominador queda una resta: 3-5.

🔔 Quinto, ya se realizo la resta y queda -2, ahora solo se vuelve a reescribir la respuesta y eso es todo.

Ejercicios para practicar

Videos para reforzar👉

Fracciones algebraicas

 Suma y resta de fracciones algebraicas homogéneas 🎫

1) Unir todo en una misma fracción (si tiene un signo negativo ubicar los números entre paréntesis)📕

2) Reducir términos semejantes📕

3) Ubicar el resultado📕

Suma y resta de fracciones algebraicas heterogéneas🎫

1) Sacar el m c m de los denominadores📗

2) Dividimos el común denominador entre los denominadores de las fracciones dadas y el resultado lo multiplicamos por el numerador correspondiente📗

3) Quitamos los parentesis📗

4) Reducimos terminos semejantes📗

5) Sacamos factor común en el numerador📗

6) Simplificamos📗

Multiplicación de fracciones algebraicas🎫

Formula básica

Multiplicacion

1) Unimos todo en una misma fraccion📘

2) Ahora factorizamos los terminos📘

3) Ahora simplificamos📘

Division de fracciones algebraicas🎫

1) Unir en una misma fraccion el numerador con denominador y el denominador con el numerador📙

2) Factorizar los terminos📙

Y quedaria📙

3) Ahora simplificamos 📙

Video sobre simplificacion de fracciones algebraicas

Ejercicios para practicar

https://www.superprof.es/apuntes/escolar/matematicas/algebra/polinomios/ejercicios-resueltos-de-fracciones-algebraicas.html#:~:text=La%20divisi%C3%B3n%20de%20dos%20fracciones,el%20numerador%20de%20la%20segunda.